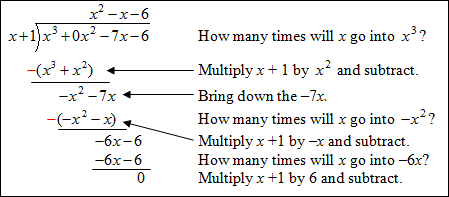POLYNOMIAL FUNCTIONS
 |
Unit Overview
Polynomial functions are important in real-world situations. For example, a polynomial function can model the relationship between the dimensions of a rectangular box and its volume. Polynomial functions can also model the volume of irregularly shaped buildings. In this unit you will identify, evaluate, add, subtract, and classify polynomials. You will also multiply and divide polynomials using long division and synthetic division. At the conclusion of the unit the Factor Theorem will be used to solve problems.
Introduction to Polynomial Functions
In studying polynomials, we will first become familiar with the vocabulary associated with polynomial functions.
monomial: a numeral, a variable, or a product of a numeral and one or more variables.
term: an expression that is a number, a variable, or the product of a number and one or more variables.
constant: a monomial with no variable, basically any number that has a constant value.
coefficient: the numerical factor of a monomial.
degree of a monomial: the sum of the exponents of the variables.
polynomial: a monomial or a sum of terms that are monomials. *Note: In a polynomial, there cannot be any variable exponents or any variables in the denominator of a term. |
Binomials and trinomials are polynomials used frequently in algebra.
binomial: a polynomial with two terms.
trinomial: a polynomial with three terms.
degree of a polynomial: the largest monomial degree of the polynomial.
leading coefficient: the coefficient of the term with the highest degree.
|
Let's review the vocabulary associated with polynomial functions.
![]() How many terms are in this expression? 3x10 + x9– 3x6– 2x3– 6x + 4?
How many terms are in this expression? 3x10 + x9– 3x6– 2x3– 6x + 4?
Six terms
"Click here" to check the answer.
![]() What is the constant term in this expression? 3x2 + 3x + 4
What is the constant term in this expression? 3x2 + 3x + 4
The constant term is 4.
"Click here" to check the answer.
![]() What is the coefficient in this expression? 6x3
What is the coefficient in this expression? 6x3
The coefficient is 6.
"Click here" to check the answer.
![]() What is the "understood" coefficient in this expression? u5
What is the "understood" coefficient in this expression? u5
The "understood" coefficient is 1.
"Click here" to check the answer.
![]() What is the degree in this monomial? 3x4y2y
What is the degree in this monomial? 3x4y2y
The degree is 7. (Recall, y is the same as y1.)
"Click here" to check the answer.
![]() What is the degree in this polynomial? –8w7 + 5w5– 2w3 –6w + 2
What is the degree in this polynomial? –8w7 + 5w5– 2w3 –6w + 2
The degree is 7.
"Click here" to check the answer.
![]() What is the leading coefficient in this polynomial? –8w7 + 5w5– 2w3 –6w + 2
What is the leading coefficient in this polynomial? –8w7 + 5w5– 2w3 –6w + 2
The leading coefficient is –8.
"Click here" to check the answer.
![]() What name is given to a polynomial with 3 terms?
What name is given to a polynomial with 3 terms?
Trinomial
"Click here" to check the answer.
When given values for variables in polynomials, evaluate them by following the rules for Order of Operations.
Example #3: Evaluate the polynomial –x2– 7x + 11 for x = 3.
The polynomial evaluates to 23 when x = 3. |
Example #4: Evaluate the polynomial 5x3– 6x2– 2x for x = –2.
The polynomial evaluates to –60 when x = –2. |
Stop! Go to Questions #1-7 about this section, then return to continue on to the next section.
Adding and Subtracting Polynomials
To add or subtract polynomials combine like terms; this means add or subtract the coefficients of any terms that have the same variable and the same exponent. Make sure the like terms are rewritten next to each other; this will make it easier to add or subtract.
Example #1: Find the sum. (6x3 + 3x2 – 4) + (10 – 3x – 5x2 + 2x3)
|
The closure properties for polynomials are very similar to those for integers. The sum, difference, or product of any two integers is an integer, and the sum, difference, or product of any two polynomials is a polynomial.
The previous example shows the closure property for addition of polynomials.
 |
When subtracting polynomials, make sure to change all the signs of the second quantity when rewriting the problem.
Example #2: Find the difference. (5x2 – 6x – 11) – (–8x3 + x2 + 2)
|
This example shows the closure property for subtraction of polynomials.
 |
Stop! Go to Questions #8-13 about this section, then return to continue on to the next section.
Products of Polynomials
To express a function in standard form means to multiply all terms together and put them in descending order (largest to smallest).
Example #1: Express the function in standard form. f (x) = (x – 1)(x + 4)(x – 3)
|
 |
Just as a quadratic expression is factored by expressing it as a product of two factors, a polynomial expression of a degree greater than 2 is factored by expressing it as a product of more than two factors.
Stop! Go to Questions #14-16 about this section, then return to continue on to the next section.
Factoring Polynomials
Just as a quadratic expression is factored by expressing it as a product of two factors, a polynomial expression of a degree greater than 2 is factored by expressing it as a product of more than two factors.
Example #1: Factor the polynomial. x3– 10x2+ 16x
Note: It is a good practice to check factoring by using multiplication.
|
| Example #2: Factor the polynomial. x3 + 6x2 – 5x – 30 This polynomial can be factored in pairs.
|
Factoring the Sum and Difference of Cubes |
The sum or difference of polynomial cubes have formulas that make the factoring simpler.
 |
Example #3: Factor x3 + 27.
The signs between the terms in the sum of cubes will always be plus (+) in the first factor and minus (–), then plus (+), in the second factor.
|
||||||||||||
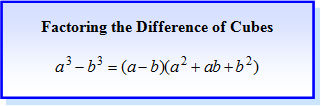 |
Example #4: Factor x3– 125.
The signs between the terms in the sum of cubes will always be plus (+) in the first factor and plus (+) for both terms in the second factor.
|
Stop! Go to Questions #17-20 about this section, then return to continue on to the next section.
The Factor Theorem
| Factor Theorem: x – r is a factor of the polynomial expression that defines the function P, if and only if, r is a solution of P(x) = 0; that is, if and only if P(r) = 0. |
What this is saying is that a binomial is a factor of a polynomial expression, if and only if, the numerical value r, when replaced for all the x values, yields 0.
Example #1: Is x – 1 a factor of f (x) = x3– x2 – 5x – 3?
This means that x – 1 is not a factor of the polynomial because f (1) ≠ 0. |
Example #2: Is x + 2 a factor of f (x) = x3 – 2x2 – 5x + 6?
This means that x + 2 is a factor of the polynomial because f (–2) = 0. |
Stop! Go to Questions #21-23 about this section, then return to continue on to the next section.
Long Division of Polynomials
Long division of polynomials is similar to long division of whole numbers, except quantities are manipulated instead of numbers.
To use long division:| 1.) | Make sure that all terms are in descending order. |
| 2.) | Make sure that all terms are represented! For example, if there is no x2 term in the polynomial, insert 0x2 for the term that is missing. This is algebraically sound because the value of 0x2 is zero and does not affect the value of the polynomial; yet, it serves as a placeholder to keep the alignment in order. |
Example #1: Divide:
|
|
Stop! Go to Questions #24-25 about this section, then return to continue on to the next section.
Synthetic Division
Another form of division is called synthetic division. Synthetic division can be used to divide a polynomial only by a linear binomial of the form x – r and only uses the coefficients of each term. (When using nonlinear divisors, use long division as discussed in the previous section.)
Example #1: Use synthetic division to find the quotient for the division problem. |
|||||||||||
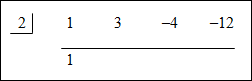
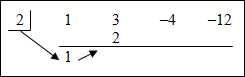
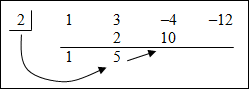
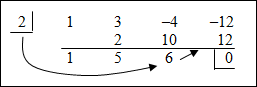
(x3 + 3x2 – 4x – 12) ÷ (x – 2) |
|||||||||||
|
|||||||||||
|
|||||||||||
| The remainder is 0, and the resulting numbers 1, 5 and 6 are the coefficients of the quotient. The quotient will start with an exponent that is one less than the dividend. 1x2 + 5x + 6 | |||||||||||
| The quotient is x2 + 5x + 6. | |||||||||||
| Thus, (x3 + 3x2 – 4x – 12) ÷ (x – 2) = x2 + 5x + 6. |
Now let’s try one that has a remainder.
| Example #2: Use synthetic division to find the quotient and remainder for the division problem. |
| Remember to bring down the coefficient of the first term of the polynomial that is being divided (1 in this case) and continue on by multiplying by the divisor (r‑value of the linear divisor) and adding. |
(x3 – 2x2 – 22x +40) ÷ (x – 4) |
 |
Since there is a remainder in this problem, the answer is written using a fraction with the divisor, x – 4, as the denominator. Notice that the sign between the last term and the fraction is the same as the sign of the remainder. |
1x2 – 2x – 14 – |
| Thus, (x3 – 2x2 – 22x +40) ÷ (x – 4) = x2 + 2x –14 – |
Division of two polynomials is not always a polynomial as is shown in this example. Therefore polynomials are not closed under the operation of division. In the fourth term of the answer, the fraction has x – 4 in the denominator. In a polynomial, there cannot be any variables in the denominator of a term.
Let's work through a division problem using synthetic division. Here is the problem.
(3x3 – 2x2 +3x – 4) ÷ (x – 3) |
![]() What number is used as the r-value to complete the division?
What number is used as the r-value to complete the division?
r = 3
"Click here" to check the answer.
![]() What are the coefficients of the polynomial?
What are the coefficients of the polynomial?
3, –2, 3, –4
"Click here" to check the answer.
![]() What are the missing numbers after multiplying and subtracting?
What are the missing numbers after multiplying and subtracting?
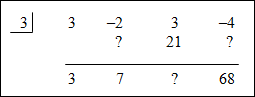
9, 24, 72
"Click here" to check the answer.
![]() What is the quotient (final answer in polynomial form)?
What is the quotient (final answer in polynomial form)?
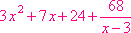
"Click here" to check the answer.
Stop! Go to Questions #26-33 to complete this unit.